What is Topology

Published: 29 Jul 2025

Topology is a fascinating branch of mathematics. It studies shapes and spaces in a unique way. Unlike geometry, topology does not care about exact measurements. It focuses on properties that stay the same even when shapes stretch or bend. Imagine a rubber band twisting without breaking that’s topology in action.

This article explores what is topology, key concepts, and real-world uses. It’s perfect for beginners curious about topology in mathematics or its applications in everyday life. Ready to dive into the world of shapes that do not tear? Let’s get started.

Table of Content

What is Topology?
History of Topology
Types of Topology
1. Topology in Mathematics
2. Topology in Computer Networks
Advantages and Disadvantages of Topology
FAQs About Topology
Conclusion

What is Topology?

Topology is a field of math that looks at how spaces and shapes connect. It studies properties that do not change when shapes stretch, twist, or bend without tearing or gluing. A topological space is a set of points with rules about how they connect. Think of it like a flexible playground where shapes can morph but keep their core features.

For example, a coffee mug and a donut are the same in topology. Why? Both have one hole! This idea, called homeomorphism in topology, shows how shapes can be equivalent despite looking different.

History of Topology

Topology studies shapes and spaces that stay the same when stretched or bent. It’s a key part of topology in mathematics, with uses in science and daily life. From ancient geometry to modern tech, topology’s history is fascinating. Let’s dive in.

Early Days of Topology

Ancient Roots and First Steps: Topology’s story begins with ancient math. Around 300 BCE, Euclid studied shapes in geometry, focusing on sizes and angles. Topology basics emerged later, caring about connections, not measurements. In the 1700s, Leonhard Euler’s Seven Bridges of Königsberg problem used topology and graph connectivity. He showed how paths connect, a key idea for topology in mathematics.

19th Century Topology Takes Shape: In the 1800s, topology became a field. August Möbius created the Möbius strip topology in 1865 a one-sided surface. Try twisting a paper strip and joining the ends! Bernhard Riemann studied topology and surfaces, like the torus topology (a donut shape). His work defined topological spaces, the core of what is a topological space.

Topology Grows: 20th Century

Formalizing the Field: In the 1890s, Henri Poincaré shaped modern topology. He started algebraic topology, using numbers to study shapes. His homotopy in topology and fundamental group topology ideas showed how loops reveal a shape’s holes. Point-set topology grew, focusing on open sets in topology and closed sets in topology.

New Branches and Ideas: Topology split into branches. General topology studied neighborhoods in topology and continuous functions topology. Geometric topology explored knot theory topology, like tangled ropes. Differential topology looked at smooth shapes. Felix Hausdorff’s separation axioms topology, like the Hausdorff space, made spaces clearer.

Topology in the Modern World

Science and Technology: In the 1900s, topology entered topology in physics, like topology in quantum physics. The Klein bottle topology, a bottle with no inside, became a fun example. Topology in computer science shaped network topology types, like star topology and ring topology, for Wi-Fi and internet.

Today’s Impact: Today, topological data analysis (TDA) and persistent homology find patterns in big data. Topology in robotics helps robots move. Topology in urban planning designs cities. Topology in art and fractal topology inspire designs. Topology in game development and topology in 3D modeling create video game worlds.

Types of Topology

Topology is not just one idea it comes in many forms depending on where and how it’s used. Some types help us understand math problems, while others show how computers and devices connect in a network. No matter the type, topology always focuses on how things are linked together, not on their exact size or shape.

Let’s break down the two most common areas where topology is used: mathematics and computer networks.

Topology in Mathematics
Topology in Computer Networks

1. Topology in Mathematics

In mathematics, topology helps people explore how shapes behave when stretched, bent, or twisted but not cut or glued. This type of study looks at spaces, surfaces, and how points connect inside them. Here are explain types of mathematics topology.

Topological Space
- A topological space is a set of points with special rules that tell which points are considered “close” or “connected.” These rules don’t need numbers or measuring tools just ideas about closeness and connection.

2. Topology in Computer Networks

Network topology is about how computers, printers, and other devices connect in a system. This is a different kind of topology, but it still studies connections and structure just like in math. There are several network topology types, each with its own layout and purpose. Here are explain types of networks topology:

Bus Topology
Star Topology
Ring Topology
Mesh Topology
Tree Topology
Hybrid Topology

Let’s explain 6 types of network topology:

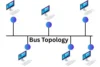
Bus Topology
- Bus topology connects all devices in a straight line using one main cable. Each device shares the same path to send and receive data. It’s easy to set up but not very strong if something breaks.

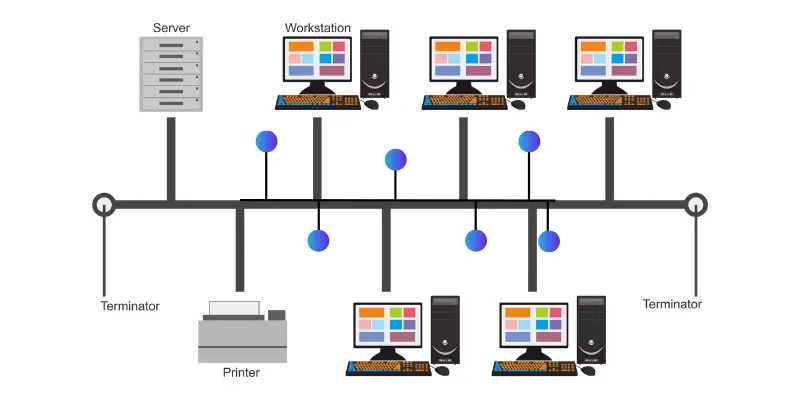
Star Topology
- Star topology links all devices to a single central hub or switch. This setup is very common in homes and schools. It’s easy to control, but everything depends on the central point.

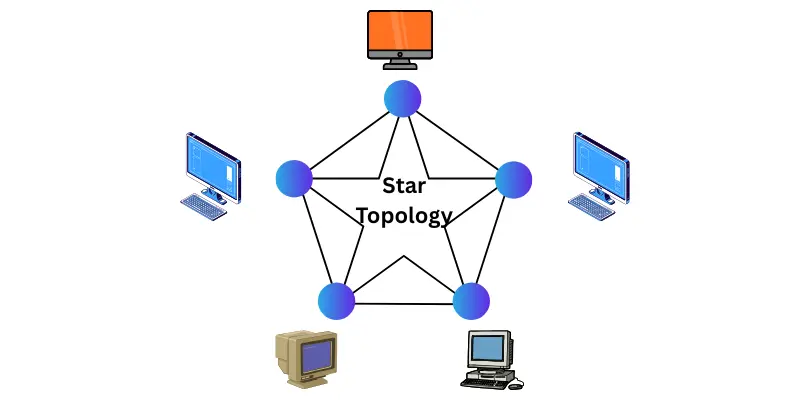
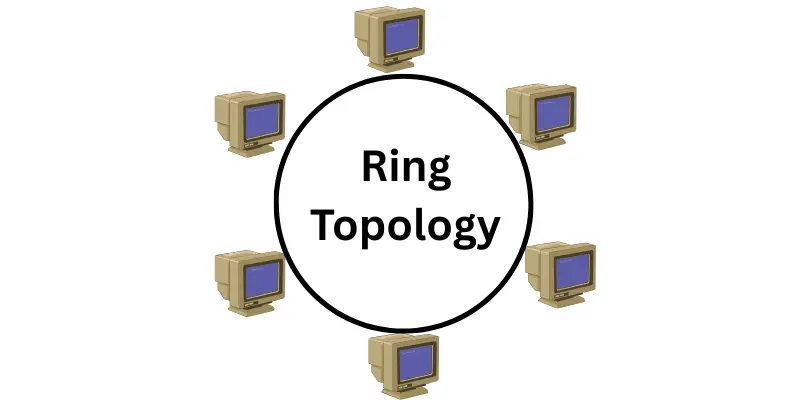
Ring Topology
- Ring topology connects devices in a circle. Each device talks to the next one in line. Data moves in one direction around the ring. If one link breaks, the whole system can stop.

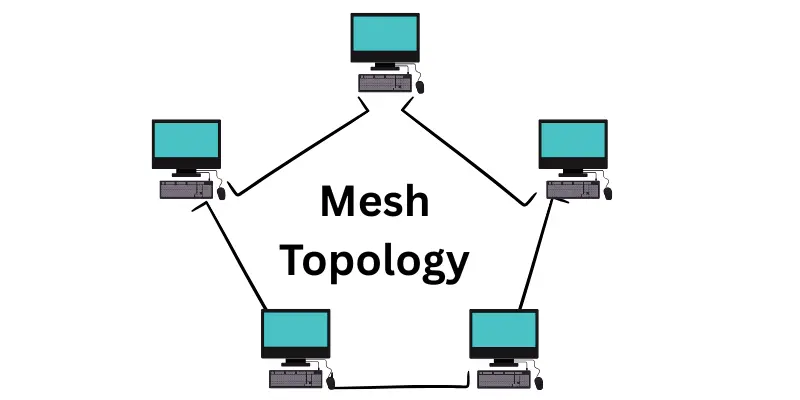
Mesh Topology
- Mesh topology connects every device to every other device. This setup gives the best strength and speed. It’s great for important systems but needs more wires and costs more.

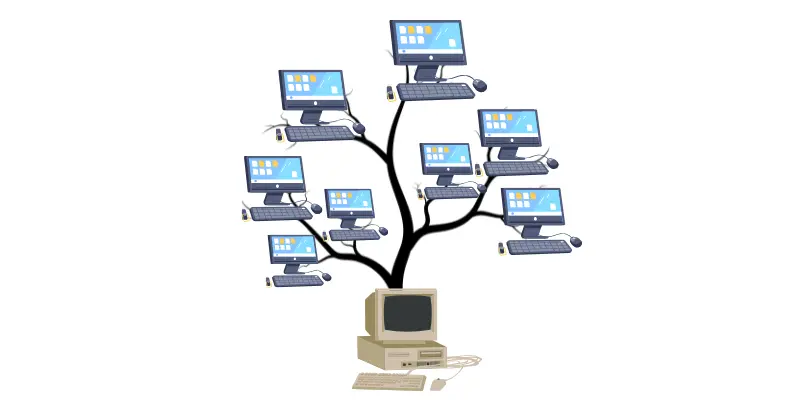
Tree Topology
- Tree topology looks like a tree with branches. It joins multiple star topologies together. It works well in big setups like schools or companies.

Hybrid Topology
- Hybrid topology mixes two or more types of network layouts. It gives flexibility and can be designed based on different needs. It’s often used in large or growing networks.

Advantages and Disadvantages of Topology

Topology, whether in math or computer networks, helps people understand how things are connected. But just like any system, it has strengths and weaknesses. Here are some simple pros and cons of topology that anyone can understand.

Advantages of Topology
Helps study shapes in new ways: Topology looks at how shapes behave when stretched or twisted. This helps in solving puzzles and complex math problems. Works without exact sizes: It focuses on connections, not measurements. This makes it easier to compare different shapes. Useful in many subjects: Topology is used in science, physics, and even robot designs. Improves system planning: Network topology helps people plan how devices should connect. Supports better data flow: Some topologies like mesh or star allow fast and safe data sharing. Easy to fix problems: In certain types like star topology, it’s easy to find and fix issues.

Advantages of Topology

Helps study shapes in new ways: Topology looks at how shapes behave when stretched or twisted. This helps in solving puzzles and complex math problems.
Works without exact sizes: It focuses on connections, not measurements. This makes it easier to compare different shapes.
Useful in many subjects: Topology is used in science, physics, and even robot designs.
Improves system planning: Network topology helps people plan how devices should connect.
Supports better data flow: Some topologies like mesh or star allow fast and safe data sharing.
Easy to fix problems: In certain types like star topology, it’s easy to find and fix issues.

Disadvantages of Topology
Can be hard to understand at first: Some ideas like topological space or open sets may confuse beginners. Too abstract for some learners: It deals with shapes that can’t be drawn or touched, which can make learning tricky. Some types are costly: Mesh topology uses lots of wires, which makes it expensive. One failure can stop everything: In bus or ring topology, if one cable breaks, the whole network might stop. Can be hard to set up: Large topologies like hybrid or tree take time and planning to build.

Disadvantages of Topology

Can be hard to understand at first: Some ideas like topological space or open sets may confuse beginners.
Too abstract for some learners: It deals with shapes that can’t be drawn or touched, which can make learning tricky.
Some types are costly: Mesh topology uses lots of wires, which makes it expensive.
One failure can stop everything: In bus or ring topology, if one cable breaks, the whole network might stop.
Can be hard to set up: Large topologies like hybrid or tree take time and planning to build.

FAQs About Topology

Many people feel confused when they first hear the word “topology.” It sounds like a hard subject, but it becomes simple when explained in easy words. Below are some of the most asked questions that students and beginners usually have about topology. These answers are short, helpful, and easy to understand even if you are learning for the first time.

How is Topology Different from Geometry?

Geometry measures exact sizes and angles. Topology ignores measurements and focuses on how shapes connect or deform, like turning a square into a circle.

What Are Some Real-Life Examples of Topology?

Topology appears in Wi-Fi networks (star topology), city planning, and even DNA studies. It helps design efficient systems and analyze data patterns.

How Can I Start Learning Topology as a Beginner?

Begin with simple ideas like open sets. Read “Topology Without Tears” or watch topology video lectures. Try drawing a Möbius strip for fun!

What Are the Applications of Topology in Technology?

Topology helps in computer networks (mesh topology), robotics navigation, and topological data analysis for big data. It makes systems smarter and faster.

Why is topology important?

Topology helps people solve problems in math, science, and computer networks. It shows how different parts of a system stay connected. It’s used in places like schools, offices, and even in space science.

Conclusion

Topology is all about how things stay connected, even when they change shape. It looks beyond size and angles and focuses on how points, lines, or devices link together.

In math, topology helps understand shapes that twist or stretch. In networks, it shows how computers and devices connect to share data. Whether it’s a rubber band or a Wi-Fi setup, topology helps explain it all.

For students and beginners, what is topology may sound tricky at first. But with real-life examples, easy words, and simple ideas, it becomes fun to learn.

Topology is not just for experts. It’s for anyone who wants to see the world in a new way by looking at how things connect.